

The first picture shows a non trivial inversion (the center of the sphere is not the center of inversion) of a sphere together with two orthogonal intersecting pencils of circles. The simplest surface (besides a plane) is the sphere. This reduces to the 2D case when the secant plane passes through O, but is a true 3D phenomenon if the secant plane does not pass through O.Įxamples in three dimensions Sphere A circle, that is, the intersection of a sphere with a secant plane, inverts into a circle, except that if the circle passes through O it inverts into a line. Any plane passing through O, inverts to a sphere touching at O. As with the 2D version, a sphere inverts to a sphere, except that if a sphere passes through the center O of the reference sphere, then it inverts to a plane. In the plane, the inverse of a point P with respect to a reference circle (Ø) with center O and radius r is a point P ', lying on the ray from O through P such that A closely related idea in geometry is that of "inverting" a point. To invert a number in arithmetic usually means to take its reciprocal.
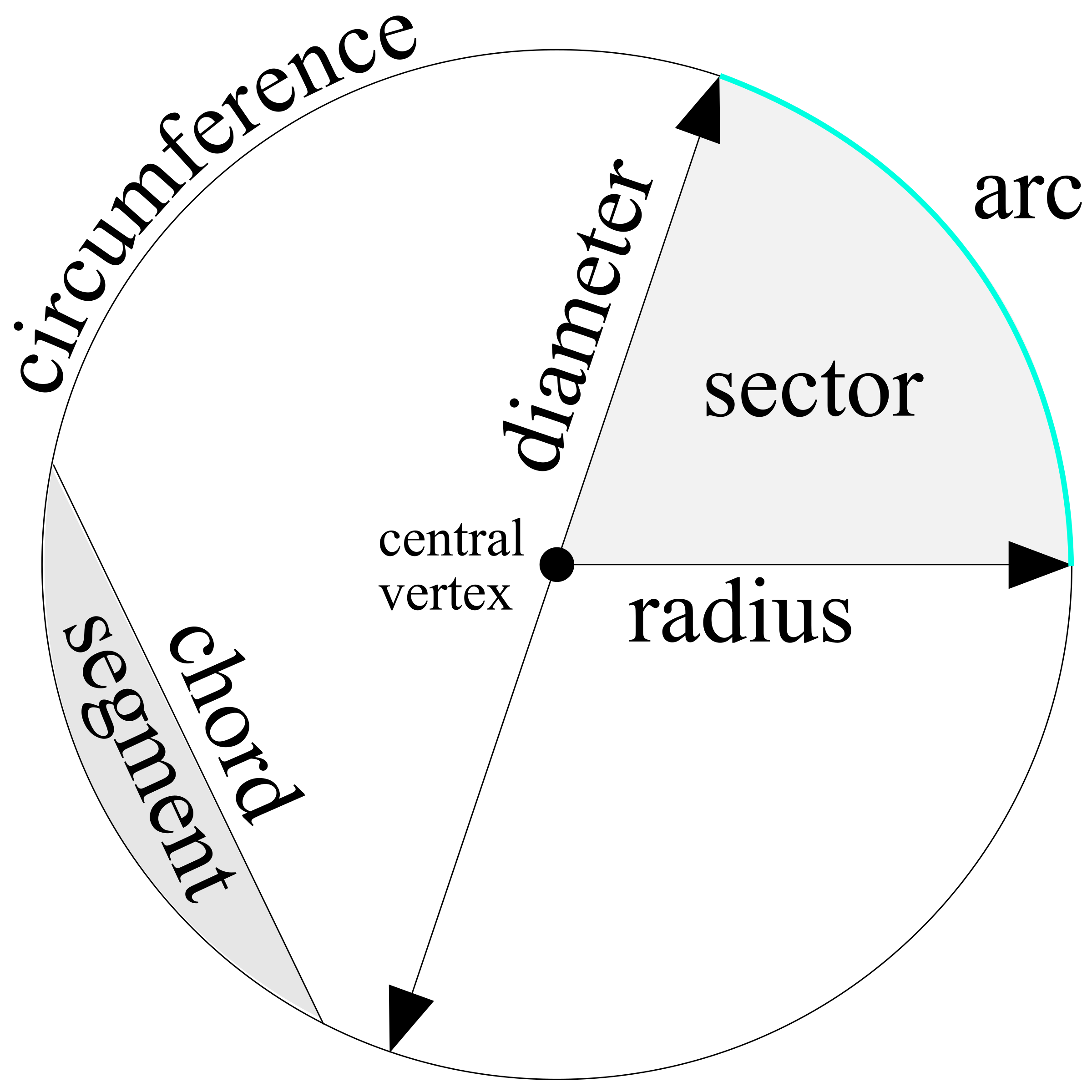
Inversion in a circle Inversion of lambda Mandelbrot set with different translations Inverse of a point P ' is the inverse of P with respect to the circle. Below we have inverted a circle, the letter ‘M,’ and a small grid across the circle C centered at z0. Example 3.2.2: Inverting Some Figures in a Circle. The concept of inversion can be generalized to higher-dimensional spaces. Inversion in the circle C centered at z0 with radius r is given by. Inversion seems to have been discovered by a number of people contemporaneously, including Steiner (1824), Quetelet (1825), Bellavitis (1836), Stubbs and Ingram (1842-3) and Kelvin (1845). Many difficult problems in geometry become much more tractable when an inversion is applied. more detailsĬonverts an instance of this class to its ArcGIS portal JSON representation.In geometry, inversive geometry is the study of inversion, a transformation of the Euclidean plane that maps circles or lines to other circles or lines and that preserves the angles between crossing curves. Removes a point from the polygon at the given pointIndex within the ring identified by ringIndex. Removes a group of handles owned by the object. more detailsĬhecks if a Polygon ring is clockwise. A statement that the most effective solution is to combine a circular plan with orthogonally planned rooms inside (Steadman,2015). Returns true if a named group of handles exist. Circular Geometry is the study of rounded shapes and their relationship to one another. Returns a point specified by a ring and point in the path. more detailsĬreates a new instance of this class and initializes it with values from a JSON object generated from an ArcGIS product. more detailsĬhecks on the client if the input point is inside the polygon. more detailsĬreates a deep clone of Circle. Show inherited methods Hide inherited methods NameĪdds one or more handles which are to be tied to the lifecycle of the object. The string value representing the type of geometry. This value defines the number of points along the curve of the circle. more detailsĬhecks to see if polygon rings cross each other and indicates if the polygon is self-intersecting, which means the ring of the polygon crosses itself.

Indicates if the geometry has z-values (elevation). more detailsĪpplicable when the spatial reference of the center point is either set to Web Mercator (wkid: 3857) or geographic/geodesic (wkid: 4326). The cache is used to store values computed from geometries that need to be cleared or recomputed upon mutation. Show inherited properties Hide inherited properties Name


 0 kommentar(er)
0 kommentar(er)
